0
Menyatakan Nilai dengan Tabel Kebenaran
Posted by Unknown
on
Kamis, Juli 03, 2014
1. Negasi
Nilai kebenaran
Jika p suatu pernyataan benilai benar, maka ~p bernilai salah dan sebaliknya jika p bernilai salah maka ~p bernilai benar.
Tabel kebenaran:
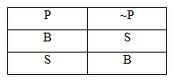
2. Konjungsi
Gabungan dua pernyataan tunggal yang menggunakan kata penghubung “dan” sehingga terbentuk pernyataan majemuk disebut konjungsi. Konjungsi mempunyai kemiripan dengan operasi irisan () pada himpunan. Sehingga sifat-sifat irisan dapat digunakan untuk mempelajari bagian ini.
Tabel Kebenaran Konjungsi :
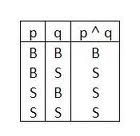
3. Disjungsi
Disjungsi adalah proposisi majemuk yang menggunakan perangkai “atau”.
Proposisi “p atau q” dinotasikan q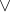 p. Tidak seperti pernyataan berperangkai “dan” yang
mempersyaratkan terpenuhinya kebenaran semua unsurnya, pernyataan
berperangkai “atau” menawarkan suatu pilihan, artinya jika paling
tidak salah satu dari kedua unsur proposisinya terpenuhi maka hal ini
sudah cukup untuk pernyataan tersebut dikatakan benar.
p. Tidak seperti pernyataan berperangkai “dan” yang
mempersyaratkan terpenuhinya kebenaran semua unsurnya, pernyataan
berperangkai “atau” menawarkan suatu pilihan, artinya jika paling
tidak salah satu dari kedua unsur proposisinya terpenuhi maka hal ini
sudah cukup untuk pernyataan tersebut dikatakan benar.
Tabel Kebenaran Disjungsi :
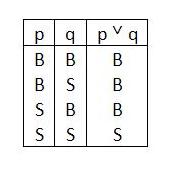
4. Implikasi
Misalkan,
p : Sore tidak hujan.
q : Elzan mengajak Gusrayani menonton.
Pernyataan “jika sore nanti tidak hujan, maka Elzan akan mengajak Gusrayani nonton”. Dapat dinyatakan sebagai “jika p maka q” atau dilambangkan dengan “p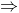 q”. Suatu pernyataan majemuk dengan bentuk “jika p maka q” disebut implikasi.
q”. Suatu pernyataan majemuk dengan bentuk “jika p maka q” disebut implikasi.
Misalkan p dan q adalah pernyataan. Suatu implikasi (pernyataan bersyarat) adalah suatu pernyataan majemuk dengan bentuk “jika p maka q”, dilambangkan dengan p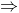 q. Pernyataan p disebut hipotesis (ada juga yang menamakan anteseden) dari implikasi. Adapun pernyataan q disebut konklusi (atau kesimpulan, dan ada juga yang menamakan konsekuen). Implikasi bernilai salah
hanya jika hipotesis p
q. Pernyataan p disebut hipotesis (ada juga yang menamakan anteseden) dari implikasi. Adapun pernyataan q disebut konklusi (atau kesimpulan, dan ada juga yang menamakan konsekuen). Implikasi bernilai salah
hanya jika hipotesis p
bernilai benar dan konklusi q bernilai salah; untuk kasus lainnya adalah benar. Perhatikan tabel berikut ini Tabel Kebenaran Implikasi :
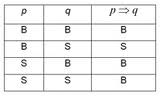
5. Biimplikasi
Misal :
Jika orang masih hidup maka dia masih bernafas
Jika seseorang masih bernafas, apakah bisa dipastikan orang tersebut masih hidup? Ya, karena jika dia sudah tidak bernafas, pasti orang tersebut sudah meninggal. Pernyataan yang demikian disebut biimplikasi atau bikondisional atau bersyarat ganda.
Pernyataan biimplikasi dilambangkan dengan “” yang berarti “jika dan hanya jika” disingkat “jhj” atau “jikka”. Biimplikasi “pq” ekuivalen dengan “jika p maka q dan jika q maka p”, dinotasikan sebagai: (p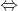 q)
q) 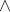 (q
(q 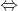 p).
p).
Misalkan p dan q adalah pernyataan. Suatu biimplikasi adalah suatu pernyataan majemuk dengan bentuk p jika dan hanya jika q dilambangkan dengan p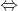 q. Biimplikasi p dan q bernilai benar jika keduanya p dan q adalah benar atau jika keduannya p dan q adalah salah; untuk kasus lainnya biimplikasi adalah salah.
q. Biimplikasi p dan q bernilai benar jika keduanya p dan q adalah benar atau jika keduannya p dan q adalah salah; untuk kasus lainnya biimplikasi adalah salah.
Tabel Kebenaran Biimplikasi :
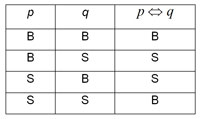
SOURCE : http://smartblogmathematic.wordpress.com/ingkaran/
Nilai kebenaran
Jika p suatu pernyataan benilai benar, maka ~p bernilai salah dan sebaliknya jika p bernilai salah maka ~p bernilai benar.
Tabel kebenaran:

2. Konjungsi
Gabungan dua pernyataan tunggal yang menggunakan kata penghubung “dan” sehingga terbentuk pernyataan majemuk disebut konjungsi. Konjungsi mempunyai kemiripan dengan operasi irisan () pada himpunan. Sehingga sifat-sifat irisan dapat digunakan untuk mempelajari bagian ini.
Tabel Kebenaran Konjungsi :

3. Disjungsi
Disjungsi adalah proposisi majemuk yang menggunakan perangkai “atau”.
Proposisi “p atau q” dinotasikan q
Tabel Kebenaran Disjungsi :

4. Implikasi
Misalkan,
p : Sore tidak hujan.
q : Elzan mengajak Gusrayani menonton.
Pernyataan “jika sore nanti tidak hujan, maka Elzan akan mengajak Gusrayani nonton”. Dapat dinyatakan sebagai “jika p maka q” atau dilambangkan dengan “p
Misalkan p dan q adalah pernyataan. Suatu implikasi (pernyataan bersyarat) adalah suatu pernyataan majemuk dengan bentuk “jika p maka q”, dilambangkan dengan p
bernilai benar dan konklusi q bernilai salah; untuk kasus lainnya adalah benar. Perhatikan tabel berikut ini Tabel Kebenaran Implikasi :

5. Biimplikasi
Misal :
Jika orang masih hidup maka dia masih bernafas
Jika seseorang masih bernafas, apakah bisa dipastikan orang tersebut masih hidup? Ya, karena jika dia sudah tidak bernafas, pasti orang tersebut sudah meninggal. Pernyataan yang demikian disebut biimplikasi atau bikondisional atau bersyarat ganda.
Pernyataan biimplikasi dilambangkan dengan “” yang berarti “jika dan hanya jika” disingkat “jhj” atau “jikka”. Biimplikasi “pq” ekuivalen dengan “jika p maka q dan jika q maka p”, dinotasikan sebagai: (p
Misalkan p dan q adalah pernyataan. Suatu biimplikasi adalah suatu pernyataan majemuk dengan bentuk p jika dan hanya jika q dilambangkan dengan p
Tabel Kebenaran Biimplikasi :

SOURCE : http://smartblogmathematic.wordpress.com/ingkaran/